Natalia Deleanu
Predarea matematicii în ciclul primar
Introducere – principii pedagogice fundamentale
În școala clasică, metodica predării oricărui obiect de studiu are la bază următoarea concepție pedagogică (și filosofică) despre procesul învățării:
Scopul învățării este să-i ofere elevului instrumentele necesare pentru a cunoaște lumea.
Instrumentele cu ajutorul cărora elevul cunoaște lumea sunt noțiunile și judecățile construite pe baza acestor noțiuni, prin procesul gândirii raționale.
Formarea noțiunilor în mintea elevului se face prin următoarele etape:
-
Prin intermediul simțurilor, elevul primește o impresie nouă (informații noi) din mediul înconjurător, care în mintea lui dă naștere la o idee. Această etapă se numește în pedagogia clasică etapa intuirii.
-
Următoarea etapă este apercepția – informația nouă este legată de fondul existent de idei și cunoștințe.
-
Etapa a treia – prin asocierea (compararea și diferențierea) noilor informații atât intre ele, cât și cu alte cunoștințe existente, iau naștere noțiunile abstracte (sau modelele mentale).
-
Noile noțiuni/modele sunt aplicate practic unui alt set de date și este verificată funcționarea și valabilitatea lor.
Pe tot parcursul acestui proces sunt respectate următoarele reguli:
-
Se lucrează la nivelul de înțelegere al elevului
-
Se asigură și stimulează atenția elevului
-
Se merge de la concret la abstract, de la simplu la complex, de la cunoscut la necunoscut
-
Sarcinile repartizate elevului sunt clare și precise
Aceste principii pedagogice au fost prezentate pe larg și detaliat în scrierile marilor pedagogi români, cum ar fi Ioan Popescu, George Radu Melidon, Ion Găvănescul, G. G. Antonescu, Ștefan Bârsănescu.
Aceleași idei se regăsesc în teoriile pedagogice occidentale, bazate pe cercetări științifice riguroase, pe teste aleatorii și controlate (randomized controlled trials), folosind tehnologii de ultimă oră de măsurare a activității creierului și organismului (electro-encefalografie, Magnetic Resonance Imaging, măsurători fiziologice).
Cea mai cunoscută dintre aceste teorii moderne, fundamentată pe aspecte unanim acceptate ale arhitecturii cognitive a omului, este teoria încărcăturii cognitive. Iată componentele principale ale acestei teorii (din articolul academic publicat online la https://link.springer.com/article/10.1007/s10648-019-09465-5):
-
Cogniția este procesul mental de asimilare a cunoștințelor și construire a înțelesului prin intermediul simțurilor, experienței și gândirii (Oxford Dictionaries).
-
Componentele arhitecturii cognitive a omului sunt memoria de lucru, memoria pe termen lung și comunicarea dintre ele.
-
Memoria de lucru (operativă) are o capacitate limitată și poate procesa un număr limitat de componente informaționale simultan.
-
Memoria pe termen lung are o capacitate aproape nelimitată.
-
Atunci când memoria operativă lucrează cu cunoștințe și abilitați stocate în memoria pe termen lung, limitările ei dispar.
-
În consecință, scopul învățării (instruirii) este de a ajuta elevii să acumuleze cât mai multe noțiuni și modele mentale în memoria pe termen lung.
-
Funcționarea memoriei operative
Există trei categorii de încărcătură cognitivă (încărcătură ce trebuie procesată în minte pentru a fi transformată în cunoaștere, în noțiuni și modele mentale):
-
Încărcătura intrinsecă
-
Încărcătura extrinsecă (superfluă)
-
Încărcătura specifică
Încărcătura intrinsecă
-
Este determinată de complexitatea informației care trebuie procesată (numărul de operații cognitive care trebuie efectuate simultan pentru procesarea informației)
Încărcătura extrinsecă (superfluă)
-
Este determinată de modul în care este prezentată informația și de ceea ce i se cere elevului să facă pe baza acestei informații
Încărcătura specifică (relevantă)
-
Este reprezentată de resursele memoriei operative necesare pentru construirea noii noțiuni, lăsând la o parte resursele irosite din cauza încărcăturii extrinseci
Pe măsură ce elevul își populează memoria pe termen lung cu noțiuni simple, pe baza acestor noțiuni se construiesc apoi modele (scheme) mentale. Aceste scheme mentale sunt apoi permanent disponibile memoriei operative și sunt înmagazinate ca unități cognitive; folosirea lor de către memoria operativă nu mai necesită procesarea fiecărei componente a schemei, deci capacitatea memoriei operative crește exponențial.
Cum se regăsesc aceste teorii și principii pedagogice în predarea matematicii în ciclul primar în România, comparând manualul din anii 1980 cu cel din anii 2020
În anii 1980 elevii intrau la 6 ani în clasa I. În anii 2020 elevii intră la 6 ani în clasa pregătitoare. Vom compara deci studierea matematicii în clasa I în anii 1980 cu studierea matematicii acum în clasa pregătitoare. În ambele cazuri este vorba de o introducere în studiul matematicii, adică de primul contact cu abstractizarea realității și de construirea unor noțiuni fundamentale precum:
-
O minge, o jucărie și un copil au în comun faptul ca pot fi reprezentate printr-o unitate (o bulină) sau printr-un semn (cifra 1)
-
Un bloc, un cubuleț, o cutie de creioane au în comun faptul că pot fi reprezentate printr-o formă geometrică (un dreptunghi)
-
Dacă punem laolaltă creioanele mele și ale tale obținem mai multe creioane (operația de adunare, semnul grafic care indică adunarea). Dacă dai din creioanele tale cuiva rămâi cu mai puține (operația de scădere, semnul grafic care indică scăderea)
Pentru un adult, a descrie formarea acestor noțiuni fundamentale pare absurd. Le folosim atât de mult în aproape fiecare clipă a vieții noastre încât ne-au devenit o a doua natură. Însă ele nu sunt niște noțiuni înnăscute; tocmai pentru că sunt fundamentale pentru viața omului și în același timp abstracte, studierea lor corectă și înțelegerea lor deplină este de o importanță covârșitoare. Fără ele, orice pași făcuți mai departe în domeniul matematicii sau al altor științe sunt sortiți eșecului.
Așadar, la clasele mici (și mai cu seamă la primul contact cu matematica) trebuie să ținem cont de următoarele aspecte:
-
Ne ocupăm cu studiul unor noțiuni fundamentale
-
Ne adresăm unui public (elevi de 6 ani) care nu a avut până acum contact cu gândirea abstractă
-
Ne adresăm unui public având capacitate de procesare limitată, cu gândirea operativă neantrenată și cu atenția scurtă
MANUALUL DE CLASA I, ANII 1980
Prima lecție pornește de la câteva obiecte și situații foarte familiare pentru școlar, prezentate în ilustrații mari și clare. La baza paginii a doua vedem două chibrituri, unul în picioare, unul culcat, și reprezentarea lor prin liniuțe orizontale sau verticale.


Astfel, pornind de la concret la abstract, se introduce ideea de reprezentare a realității prin forme sau simboluri. Urmează câteva pagini în care se introduc diferitele forme geometrice de bază. Apoi, prin același fel de analogii, sunt prezentate semnul plus, semnul egal.
Urmează desenarea de componente ale cifrelor, similară cu exersarea componentelor literelor de mână la română (cârligașe care seamănă cu un cârlig de macara etc). În paralel se studiază corespondența mulțimilor – opt muncitori cărora le corespund opt roabe, șapte fetițe cărora le corespund șase flori, deci una rămâne fără floare. Se introduce astfel în mod treptat conceptul de „mai mic”, „mai mare”. Trebuie să creeze și elevii corespondențe – de exemplu să deseneze câte o bulină pentru fiecare fluturaș dintr-o mulțime. Astfel se fac primii pași pe calea abstractizării.
Toată această activitate se desfășoară pe 13 pagini de manual (aproape a zecea parte din cele 159 de pagini). Elevul nu scrie altceva decât liniuțe și cârligașe și nu citește nici un cuvânt tipărit.
Introducerea numerelor 0-9 și a cifrelor cu care sunt scrise
Fiecare număr este tratat pe o pagină de manual, prin desene foarte clare. La baza paginii sunt trasate cifra, mare, și un obiect căruia i se aseamănă. Pe măsură ce ajungem la numere mai mari, le prezentăm prin comparație cu cele mai mici. Vedem și cum se poate forma fiecare număr din alte numere. De asemenea, numerele mai mari le reprezentăm din ce în ce mai puțin prin obiecte concrete și din ce în ce mai mult prin mulțimi de buline. Avem în manual și ilustrații cu barele tip lego de diferite lungimi și culori (care existau ca material didactic ajutător).


Prezentarea celor 10 cifre și a numerelor 0-10 ocupă 19 pagini de manual (mai mult de o zecime). Se trece la ordonarea crescătoare și descrescătoare a numerelor învățate, care începe cu o privire de ansamblu (toate cele zece numere, reprezentate prin sârme cu numărul respectiv de bile, în ordine, trenulețul numerelor, cu toate numerele în ordine). Apoi se trece la secvențe de câte trei sau cinci numere care trebuie scrise în ordine. Exersăm separarea unei mulțimi în două submulțimi.
Adunarea numerelor 0-10 fără trecere peste ordin (peste 10)
Se trece la adunarea cu 1. Pe patru pagini de manual, fiecare număr de la 1 la 9 este adunat cu 1, folosind animale, bile de numărătoare și bare de lego, pentru a arăta vizual corespondența. Noțiunile sunt introduse metodic. Se merge mereu pe observația vizuală, pe reprezentarea grafică a operațiilor, pentru ca elevul să poată sesiza asemănările și deosebirile (bara de 5 are o pătrățică în plus față de bara de 4, daca adăugăm o pătrățică la bara de 7 vedem că devine egală cu bara de 8). Reprezentările grafice ale numerelor sunt mereu așezate în ordinea lor logică (crescătoare sau descrescătoare). Astfel se facilitează procesul cognitiv (observare/intuire, alăturare, comparare, extragerea noțiunilor fundamentale).
Ilustrațiile sunt mari și clare, bine organizate, puține pe o pagină, înconjurate de mult spațiu alb, ceea ce facilitează concentrarea atenției și procesarea informației. Încărcătura cognitivă este mică, perfect calibrată pentru mintea elevului de 6 ani. Practic nu există încărcătură excedentară/inutilă.


Urmează scăderea cu 1, prezentată la fel (întâi concret, apoi cu bare lego, toate scăderile cu 1 scrise în paralel cu adunările corespunzătoare). Urmează, similar, adunarea și scăderea cu 2. Apoi este introdus, pe trei pagini, numărul 0, adunarea/scăderea cu 0, operații cu rezultat 0 (conceptul de „nimic” fiind mai dificil dar deosebit de important mai târziu la scrierea numerelor cu zeci, sute mii etc).
Continuăm cu adunarea/scăderea cu fiecare număr de la 3 la 9. Fiecare ocupă patru pagini de manual și include și exerciții din adunările/scăderile precedente. Întreaga secțiune se încheie cu tabla adunării și tabla scăderii. Secțiunea dedicată adunării și scăderii ocupă aproape 20% din manual.
Urmează:
-
Proba adunării prin scădere (5 pagini)
-
Adunări de trei termeni (fără trecere peste 10) (2 pagini)
-
Probleme recapitulative (3 pagini). Jumătate au enunțul pe bază de ilustrații, jumătate sunt scrise ca exerciții. În total sunt 23 de probleme și exerciții.
-
Metrul, litrul, leul și operații simple cu mărimi exprimate în m, l, lei (4 pagini)

Studiul zecilor
Începe la pagina 80 (adică exact la jumătatea manualului). Se pune de la început accentul pe organizare:


Trecem apoi la analogia dintre operațiile cu numere formate numai din unități și operațiile cu numerele formate numai din zeci (3+2=5, 30+20=50). Astfel, pornim de la ceea ce elevul știe deja și-i arătăm că poate aplica același model mental de adunare într-un context diferit, dar analog. Elevul învață să efectueze operații cu numere mari (70, 80), care altminteri ar necesita o încărcătură mare a memoriei de lucru, extrăgând din memoria pe termen lung modelul operației cu unități. În același timp, prin ilustrații, facem foarte clară diferența dintre zeci și unități, care poate prezenta dificultăți mai apoi, când vom ajunge la numerele formate și din zeci, și din unități.


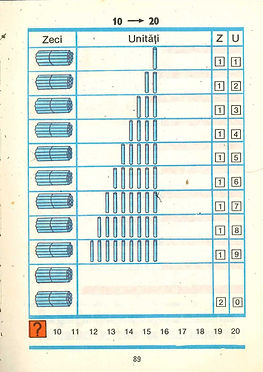
Numerele formate din zeci și unități (dintre 10-20)
Construind pe conceptele asimilate până acum, prezentăm numerele acestea în mod structurat – cu o zece grupată separat, unitățile alături. Se observă astfel foarte clar că numerele de la 10 la 20 sunt exact ca numerele de la 0 la 10, numai că au un mănunchi de zece bețișoare în față. Arătăm că se pot reprezenta în diverse forme (cu bețișoare, cu bare lego, cu sticle așezate în lăzi de câte zece, cu numărători). La sfârșit avem un tabel 10x10 cu toate numerele de la 0 la 10 organizate pe rânduri și coloane, pentru a putea urmări legătura logică dintre ele și a avea un tablou complet a ceea ce am învățat până acum.
Adunarea și scăderea de numere cuprinse între 10-20 cu numere mai mici decât 10, fără trecere peste ordin
Așa cum am învățat că 3+2=5, acum vedem că putem face 13+2= 10+3+2=10+5=15. Plecând de la modelul mental simplu al adunării de unități (numere sub 10) și de la descompunerea unui număr în zeci și unități, pe care le-am studiat separat, aplicăm aceste metode acum combinat și rezolvăm un exercițiu mai greu.
Analog, ca să scădem 20-6, descompunem pe 20: 20-6=10+10-6=10+4=14. Introducem astfel și ideea “împrumutării” unei zeci (cu care mulți copii au dificultăți), care ne va folosi foarte mult mai târziu, la scăderea cu trecere peste ordin.
Se trece apoi la scăderi de numere cu două cifre din numere cu două cifre, fără trecere peste ordin (15-11, 17-14). Și aceste operații le efectuăm folosind noțiunile deja învățate.
Urmează șase pagini de exerciții și probleme. Pentru prima dată (la pagina 109 din 159) sunt introduse exerciții tip tabel, în forma lor cea mai simplă (cu o singură coloană).
Adunarea/scăderea numerelor formate din oricâte zeci și unități cu numere formate din unități (34+3=37) – prezentate prin analogie cu ce știe deja elevul.
Adunarea/scăderea numerelor formate din oricâte zeci și unități cu numere formate doar din zeci (34+30=64) – prezentate prin analogie cu ce știe deja elevul.
Urmează patru pagini de exerciții și probleme, cu mai puține ilustrații. Se introduce kg, cu exerciții asemănătoare celor de la metru și litru. Se studiază ceasul și măsurarea timpului.

Urmează 15 pagini de exerciții și probleme recapitulative. Se cere compararea numerelor la unele dintre ele, însă prin notarea în cuvinte „este mai mic decât”, „este mai mare decât”, „este egal cu”.
La sfârșit avem patru pagini de exerciții și probleme diverse, unde se cere completarea de tabele 3x3 sau 4x4, completarea de șiruri, se introduc tehnici de grupare pentru adunări de mai mulți termeni – exercițiile cele mai grele de până acum, care ne arată din nou cum am putea combina modele și tehnici de calcul învățate separat pentru a rezolva exerciții mai dificile.
Concluzii
-
Prima jumătate a manualului (80 de pagini) este dedicată numerelor 0-10 și operațiilor de adunare/scădere sub 10. Aceasta ne arată importanța covârșitoare a înțelegerii și fixării corecte a acestor noțiuni. Tot ce se studiază ulterior se construiește pe ele, atât în clasa I, cât și la clasele următoare. Orice gol sau înțelegere vagă a uneia din aceste noțiuni de bază are repercusiuni uriașe mai târziu. Pe de altă parte, o bună înțelegere și fixare a lor duce la incorporarea acestor noțiuni în memoria pe termen lung și reutilizarea lor fără efort la orice moment din viitor.
-
Metoda de predare și lucru – se avansează cu pași mici, dar siguri, nu în salturi. Se trece de la simplu la complex prin combinarea de noțiuni simple, deja asimilate. Toată materia este ancorată în obiecte concrete, familiare elevului. Se pune accentul pe organizarea vizuală și conceptuală a materiei, pe prezentarea constantă a noilor informații alături de cele deja asimilate, pentru ca elevul să poată sesiza asemănările și diferențele. La încheierea unei unități de studiu, se prezintă elevului „harta” cunoștințelor din acea unitate (tabelul numerelor 0-100, tabla adunării, tabla scăderii).
-
Atenția și interesul elevului sunt captate și reținute în multe feluri:
-
Prin raportarea permanentă la mediul familiar al elevului.
-
Prin solicitarea unor eforturi care corespund capacității cognitive a elevului (orice elev se plictisește dacă nu înțelege; dacă munca elevului este încununată de succes, aceasta stimulează încrederea în sine și satisfacția că e bun la învățătură)
-
Prin ilustrații cu o grafică și structură vizuală clară, simplă, care facilitează concentrarea atenției și nu includ elemente superflue, pur decorative, care nu ajută procesului de învățare
MANUALUL DE MATEMATICĂ ȘI EXPLORAREA MEDIULUI PENTRU CLASA PREGĂTITOARE (Editura Joy, 2014)
(pentru ca analiza să fie clară și relevantă, vom lăsă la o parte secțiunile din manual dedicate preponderent explorării mediului și vom comenta abia la sfârșit efectul lor asupra procesului de învățare)
Manualul se deschide cu patru pagini de evaluare inițială. Fiecare pagină include 4-5 exerciții, fiecare identificat printr-un buton tridimensional, de culoare diferită. Exercițiile sunt alcătuite din enunțuri scrise și ilustrații. Se remarcă două lucruri:
-
De pe prima pagină, de la primul contact cu matematica, apar exerciții unde i se cere elevului să facă lucruri pe care nu le-a învățat încă (să citească un enunț tipărit, să recunoască și să scrie cifre). Elevul de CP (clasa pregătitoare) încă nu a învățat să citească, deci enunțurile scrise îl pot debusola și-l pot face să se simtă inadecvat (chiar dacă sunt citite de învățător). Iar cifrele va învăța să le recunoască și să le scrie mai târziu (secțiunea Numerele 0-10).
-
Exercițiile sunt propuse în ordine inversă dificultății (mai întâi apar exerciții mai grele, apoi unele mai ușoare). De exemplu, la începutul evaluării elevul trebuie sa unească un număr de lumânări cu cifra corectă, sau chiar să scrie el cu cifre numărul unor obiecte, iar pe ultima pagină de evaluare i se cere să traseze într-un cadran atâtea liniuțe câte obiecte sunt desenate.
Aceste deficiențe se regăsesc pe tot cuprinsul manualului.


Urmează 12 pagini de Orientare și localizare în spațiu și apoi Mănânc sănătos, combinată cu scrierea de liniuțe verticale, orizontale, oblice, de pătrate, triunghiuri, cerculețe, semne de plus, egal, înmulțit, și cu recunoașterea figurilor geometrice plane.
Numerele 0-10
Pe parcursul a 34 de pagini, traversăm următoarele etape cognitive:
-
Învățăm numerele 1-5 și cifrele 1-5
-
Învățăm numărul și cifra 0
-
Învățăm numărul și cifra 6
-
Recapitulăm numerele 0-6
-
Învățăm numărul și cifra 7
-
Recapitulăm numerele 0-7
-
Învățăm numerele 7-10 și cifrele 7-9
-
Recapitulăm numerele 0-10
Deficiențele acestei secțiuni:
-
O deficiență majoră este că autorii nu par a face diferența între cifră (semn grafic, folosit în matematică pentru a scrie numere așa cum litera este folosită la română pentru a scrie cuvinte) și număr (mod de a reprezenta cu ajutorul cifrelor o cantitate). Întâlnim mai multe exerciții de felul următor, în care „număr” și „cifră” sunt folosiți interșanjabil:


Această confuzie conceptuală propagată chiar de manual are repercusiuni extrem de grave mai târziu, când elevul învață despre numere alcătuite din mai multe cifre, unde trebuie să facem distincții foarte importante între cifra de pe locul zecilor, cifra de pe locul sutelor, ș.a.m.d. Un elev care rămâne cu confuzia între cifre și numere nu poate depăși conceptual matematica de clasa I.
-
Încărcătura cognitivă extrinsecă (inutilă pentru procesul de formare a noțiunilor) este foarte mare, din următoarele motive:
-
Ilustrațiile sunt haotice, de stiluri grafice complet diferite și amestecate. Avem pe aceeași pagină ilustrații de oameni, animale, plante, obiecte și cifre, reprezentate tridimensional, bidimensional, prin simboluri (stickman) sau contururi (line drawing), unele cu extrem de multe detalii și culori, altele foarte rudimentare. Pentru a rezolva un exercițiu cu o cerință simplă („scrie numărul corespunzător mulțimii de obiecte”), elevul trebuie mai întâi să proceseze mental fiecare obiect grafic. Fiecare frunză, legumă, copac etc este reprezentată printr-un alt fel de ilustrație, de la un exercițiu la altul sau chiar în cadrul fiecărui exercițiu. Elevului nu i se permite niciodată să decodifice vizual o ilustrație și apoi să o reîntâlnească, pentru a o putea recunoaște rapid și procesa mai ușor („Aha, asta e o frunză, mi-o amintesc de la exercițiul precedent!”) Nivelul de încărcătură cognitivă inutilă este incredibil de mare.
De altminteri, aceasta este o problemă comună marii majorități a manualelor și auxiliarelor de pe piața românească. Autorii pornesc de la presupunerea (complet eronată) că haosul vizual stimulează interesul elevului. Nici unul din autori nu pare a fi auzit de teoria încărcăturii cognitive, deși ea a apărut încă din anii ’70 și este studiată la toate programele de „learning science” din Occident. În schimb, după cum am văzut, problema aceasta a ilustrațiilor care împiedică învățarea nu există în manualul din anii ’80.


-
Exercițiile combină în mod inutil două cerințe simple, încărcând astfel memoria operativă a elevului fără ca el să învețe ceva în plus. De exemplu, exercițiul următor:

Pentru a rezolva cerința, elevul trebuie să facă două lucruri deodată:
-
Să aleagă o culoare.
-
Să compare toate numerele scrise cu culoarea respectivă.
-
(să reînceapă procesul cu altă culoare)
Dacă scopul exercițiului este ca (1) elevul să știe să recunoască culorile, și (2) ca elevul să știe să compare numerele până la 10, ce câștigă elevul prin faptul că trebuie să opereze simultan cu ambele cerințe? Ambele scopuri pot fi atinse la fel de bine (chiar mai bine) prin două exerciții separate.
Dacă scopul este ca elevul să identifice singur pașii de rezolvare a unui exercițiu complex, această sarcină este nepotrivită pentru vârsta de 6 ani. Elevul care abia pătrunde în lumea matematicii și abia învață cifrele nu este pregătit din punct de vedere cognitiv să recunoască algoritmi de calcul și să opereze cu ei (parcurgerea aceleiași succesiuni de etape, de fiecare dată cu un set diferit de date, se numește algoritm). De altminteri, in programa CP în vigoare nu se menționează nicăieri introducerea algoritmilor.
Din nou, singurul rezultat al împovărării copiilor cu două cerințe simultane este supraîncărcarea memoriei operative în mod inutil și păgubos. Acest exercițiu nu reprezintă un caz izolat; toate manualele și auxiliarele pe care le-am consultat includ în mod repetat exerciții în care elevului i se cere să opereze simultan cu cerințe multiple; cerințele simultane devin din ce în ce mai dificile și mai numeroase la clasele I și mai departe.
-
Datorită necesității de a integra studiul matematicii cu al altor materii (științele naturii etc), autorii ajung să propună exerciții absurde din punct de vedere logic și supraîncărcate cognitiv, din care elevul nu învață de fapt nimic în plus. Iată un exemplu:

-
Lipsa de coerență în folosirea ilustrațiilor.
-
Ilustrațiile sunt folosite arbitrar. De exemplu, la majoritatea exercițiilor contează numărul obiectelor ilustrate: elevul trebuie să scrie câte flori sunt într-o mulțime, sau să noteze într-un tabel numărul electrocasnicelor, pe categorii; trebuie să coloreze primul, al treilea și al șaselea arici dintr-un șir. Deci el va trage concluzia ca că există o legătură între numărul obiectelor și cerința exercițiilor.
Însă printre aceste exerciții avem altele, unde ilustrația este doar un pretext, cum ar fi următorul:

Aici nu mai contează numărul obiectelor ilustrate; ele servesc doar de pretext pentru a da elevului o sarcină (să indice numărul mai mare colorând frunza corespunzătoare). Nu mai există corelația număr – ilustrații (avem doar o frunză, cu diverse numere pe ea). Din punct de vedere al învățării, același rezultat poate fi obținut cerând elevului să înconjoare numărul mai mare.
-
Ilustrațiile sunt pur decorative. În alte exerciții, ilustrațiile nu folosesc la absolut nimic, nici măcar ca pretext de rezolvare a unei cerințe. De exemplu:

Prezența tuturor acestor specii de ciuperci nu contribuie cu nimic la rezolvarea exercițiului; ea nu face decât să consume din resursele cognitive ale elevului (deoarece creierul este programat să proceseze orice element vizual care i se înfățișează). Mai mult decât atât, grupurile de câte trei numere nu sunt suficient separate vizual și atunci apar ca un lung șir presărat cu ciuperci. Elevul trebuie să stea să descifreze mai întâi dacă nu cumva exercițiul prezintă un șir care trebuie completat, deoarece în manual există frecvent și exerciții de acel gen. Nu era mai simplu și mai clar să eliminăm ciupercile și să prezentăm grupurile clar separate câte trei?
-
O ultimă deficiență pe care o vom menționa aici este că exercițiile nu merg de la simplu la complex, ci de multe ori elevul se confruntă cu cerințe înainte de a învăța să le rezolve, sau cu cerințe mai grele la început și altele mai ușoare la sfârșit. De exemplu, la lecția dedicată numărului 5 se cere elevului să compare perechi de numere și să decidă care e mai mare/mai mic, însă abia peste câteva pagini este introdusă conceptual ideea comparării a două numere prin stabilirea corespondenței elementelor a două mulțimi. De asemenea, în mod bizar, deși am arătat că manualul are numeroase exerciții dificile, cel mai simplu exercițiu de până acum este ultimul din această secțiune:

Menționăm acest lucru deoarece el face parte dintr-o tendință mai amplă a autorilor de manuale alternative/reformate (pe care am regăsit-o inclusiv la probleme de fizică de clasa a VII-a, de exemplu), de a începe cu cerințele cele mai grele și a termina cu cele mai ușoare, mergând astfel în mod flagrant împotriva oricăror metode și teorii pedagogice valabile.
Adunarea și scăderea cu 1-5 în concentrul 0-10 (15 pagini)
Problemele descrise până acum sunt prezente în continuare. Avem ilustrații care sporesc gradul de confuzie a elevului: de exemplu, deși la majoritatea exercițiilor se adună obiecte identice, la unele exerciții se adună iepuri cu vulpi, trandafiri cu inimi, bascheți cu ciori. Avem ilustrații inutile (“Găsește numerele ascunse sub bulgări”). Avem exerciții unde legătura dintre ilustrație și operația cerută este neclară (un pinguin care plutește cu parașuta, sub el scriind 1+1= __, o fetiță care o împinge pe alta pe sanie sub care scrie 1+2=__; probabil că, în intenția autorilor, e vorba de un pinguin plus o parașută și două fetițe plus o sanie, dar intenția autorilor e greu decelabilă pentru copii).



Cea mai mare deficiență a acestei secțiuni este însă că se oprește la adunarea cu 5. Acest aspect se datorează programei, care prevede, la CP, Competențe specifice și conținuturile învățării, „Efectuarea de adunări și scăderi în concentrul 0-31, prin adăugarea/extragerea a 1-5 elemente dintr-o mulțime dată” și, la Conținuturi, „Adunarea și scăderea în concentrul 0-31, fără și cu trecere peste ordin, prin numărare/cu suport intuitiv”.
Am putea să ne închipuim că Ministerul Educației a limitat învățarea adunării și scăderii numai până la 5 din grijă pentru elevi, ca să nu-i obosească cu numere prea mari. Această presupunere dispare imediat ce observăm că, 20 de pagini mai târziu, elevii învață adunarea în concentrul 0-20 cu trecere peste ordin (cum ar fi 7+5, cu trecere peste 10), iar câteva pagini mai târziu, adunarea cu trecere peste ordin până la 31. Suntem deci siliți să tragem concluzia că nu se învață adunarea cu 6, 7, 8 și 9 deoarece se consideră că ea a fost deja “acoperită” în cadrul adunării cu 1, 2, 3, 4 și 5, prin exerciții de genul 6+1, 7+2. Ministerul uită că elevilor de CP nu li s-a predat formal noțiunea de comutativitate (că 6+1=1+6), și că studierea adunării cu toate numerele de la 0 la 9, pe rând, contribuie exact la înțelegerea intuitivă a noțiunii de comutativitate. În plus, un elev care are foarte clară în minte tabla adunării va înțelege și reține foarte ușor care sunt perechile de numere a căror sumă este 10, noțiune esențială ulterior, la învățarea adunării cu trecere peste ordin.
Numere formate din zeci și unități
Deci, după ce adunăm ceva numere cu 5, trecem direct la numere formate din zeci și unități. Lipsește complet secțiunea adunărilor de numere formate numai din zeci, prezentate analog cu adunarea de unități (2+3=5, 20+30=50).


Urmează trei pagini pe care autorii se străduiesc din greu să arate grafic cum din zece unități se formează o zece – și eșuează lamentabil. Avem o pagină întreagă de cadrane. În fiecare cadran avem două coloane: una pe care se repetă de 10 ori un obiect greu identificabil, urmat de un oval care arată ca o fasolă verde. Sub coloana de 10 fasole verzi observăm ilustrația minusculă a unei mâini cu deget acuzator îndreptat în jos, către ceva care arată ca o fasolă roșie. Alături e o altă coloană, pe care obiectul neidentificat și fasola verde se repetă de mai puțin de 10 ori.
Din această harababură vizuală, elevul trebuie să înțeleagă că zece fasole verzi sunt înlocuite cu o fasolă roșie, care acum se numește “o zece”.
Autorii manualului din anii ’80 rezolvau reprezentarea vizuală a zecilor mult mai elegant. Un triunghi albastru era umplut cu zece buline negre, elevii înțelegeau că acesta reprezintă o zece, și apoi triunghiul albastru era folosit direct, fără a mai pune bulinele negre în burta lui. Această metodă era introdusă în clasa a II-a, când se învățau adunarea și scăderea cu trecere peste ordin.

În manualul nou urmează adunarea și scăderea în concentrul 0-20, fără trecere peste ordin (de ex. 12+4). Acest tip de adunare nu se face aici prin separarea zecii și adunarea mai întâi a unităților, ca în anii ’80. Practic, numerele dintre 10 și 20 sunt tratate la fel ca numerele sub 10. Elevul adună 12 cu 4 numărând elementele mulțimii finale, deși ar fi mult mai simplu să folosească cele două procedee învățate deja – să descompună 12 în o zece și 2 unități, să adune 2+4=6, să adauge zecea la unități. Metoda numărării (recomandată de Minister) merge complet împotriva principiului de a valorifica modelele mentale deja asimilate, pentru învățarea de operații noi, mai dificile. Elevului i se cere doar să numere în neștire numere mari (17, 18, 19), pe care nici măcar nu le poate cuprinde pe cele două mâini.
Numerele dintre 20-31, adunarea și scăderea fără și cu trecere peste ordin
Se procedează ca și până acum, adică elevul trebuie să numere până la 25 pentru a aduna pe 18 cu 7, sau de la 25 înapoi la 18 pentru a scădea pe 7 din 25. O abordare inutilă și chiar nocivă, deoarece în anul următor, la clasa I, se studiază adunarea cu trecere peste ordin prin completarea unei zeci, și scăderea cu trecere peste ordin prin împrumutarea unei zeci. Introducerea adunării și scăderii cu trecere peste ordin la CP constituie și ea o încărcare inutilă a programei, care contravine tuturor teoriilor pedagogice valabile și nu servește la nimic, decât să ocupe timpul elevului, să-l frustreze și să-l lase cu convingerea că matematica e ceva greu și plictisitor.
Urmează 30 de pagini de exerciții și probleme de același fel, cu fasole verzi și roșii care nu te ajută cu nimic să rezolvi mai ușor operațiile cu numere până la 31, și operații cu numere până la 31 făcute prin numărare tâmpă, la care invariabil elevul se încurcă și e silit s-o ia de la capăt. Intervin din ce în ce mai mult exercițiile tip tabel, adică de descoperire și aplicare a unui algoritm.

De exemplu, completarea tabelului alăturat cere elevului să-și dea seama singur că trebuie să parcurgă următoarele etape:
-
Să citească primul număr de pe coloana din stânga
-
Să scadă din el primul număr de pe rândul de sus (majoritatea scăderilor fiind cu trecere peste ordin, deci mai dificile)
-
Să treacă rezultatul în căsuța aflată la intersecția rândului și coloanei pe care se află aceste numere
-
Să o ia de la capăt cu numerele următoare
Spre deosebire de alte exerciții, cu enunțuri lungi și elaborate, tabelele au doar enunțul „Calculează”. Toate operațiile necesare completării tabelului trebuie făcute în minte. Faptul că prezentarea grafică și enunțul exercițiului sunt extrem de simple îl poate face să creadă pe elev că rezolvarea este ușoară, ceea ce este înșelător. Toate aceste aspecte contribuie la creșterea gradului de confuzie al elevului și la încărcarea inutilă a procesului cognitiv.
Manualul se încheie cu 30 de pagini de exerciții în care se amestecă forme geometrice, tabele cu diverse obiecte, grafice, șiruri, bani, reciclare, zilele săptămânii, labirinturi, lunile anului, starea vremii. Pe ultimele două pagini avem evaluarea finală, din care ar trebui să ne putem da seama ce trebuie să știe un elev la sfârșitul clasei pregătitoare. După cum ne-am obișnuit deja, aceste exerciții de la sfârșit sunt mult mai simple decât majoritatea exercițiilor lucrate pe parcursul manualului, cel mai dificil fiind 18-3=__.

(Tabel comparativ pentru partea de numerație din cele două manuale, unde intervin diferențele cele mai grave)

Concluzii
1. Deficiențe legate de programă
-
Programa nu urmărește deloc formarea de modele mentale pe baza cărora să se predea concepte și operații din ce în ce mai grele. Faptul că elevul învață să adune pe 7 cu 3 nu e folosit pentru a-l învăța să adune pe 17 cu 3, pe 47 cu 3 sau pe 70 cu 30. Pur și simplu se adună numerele 1-30 cu numerele 1-5, fără și cu trecere peste ordin. Se învață transformarea unităților în zeci, dar nu se clădește nimic pe ea, deoarece adunarea cu trecere peste ordin nu se face prin completarea unei zeci, ci prin numărare.
-
Elevului nu-i este niciodată clar ce-a învățat și ce n-a învățat. Materia este alcătuită dintr-un lung șir de adunări și scăderi presărate cu informații disparate și nestructurate despre școală, anotimpuri, plante, animale, România, tradiții, mijloace de transport, meserii, sărbători, cosmos, medii de viață, circul, grădina zoologică, muntele și marea. Aceste informații (care nu ajung niciodată cunoștințe, noțiuni) sunt transmise prin intermediul ilustrațiilor. De multe ori ilustrațiile de fapt nu corespund temei, ca de exemplu la pagina de Meserii – Unde și vibrații, unde avem exerciții de numărare pe mulțimi de foarfeci, seringi, șuruburi și piepteni (din care nici unul nu vibrează). Varietatea și incoerența subiectelor legate de „mediul înconjurător” pare a avea ca scop mai degrabă posibilitatea de a varia la nesfârșit ilustrațiile, pe principiul „dacă arată altfel, atrage atenția elevului”.
2. Deficiențe legate de manual
-
Utilizarea unei cantități covârșitoare de ilustrații haotice, arbitrare sau inutile; lipsa completă de organizare vizuală a informației, supraîncărcarea permanentă a memoriei operative a elevului cu informații vizuale inutile.
-
Lipsa de gradare a dificultății cerințelor și lipsa de corelare a cerințelor cu cunoștințele elevului
-
Propunerea de exerciții în care se combină algoritmic mai multe cerințe simple, astfel încât elevul nu învață nimic în plus dar i se supraîncarcă memoria operativă în mod inutil
Practic, un elev care studiază matematica după această programă și acest manual este confruntat la fiecare lecție cu un „maldăr” de biți de informație, foarte puțin structurată, din care pe de o parte nu-și poate clădi modele mentale pe care să se sprijine mai târziu, dar care, pe de altă parte, sunt greu de procesat din cauza încărcăturii cognitive inutile. Este un mod complet neproductiv și nociv de a introduce un elev în studiul matematicii, care nu poate duce decât la frustrare, eșec și ideea că „matematica e prea grea pentru mine”.
Reforma structurală și mai apoi sistemică a sistemului de învățământ din România, reformă inițiată în 1992, a avut în vedere alterarea totală (”sistemică”) a școlii românești. Traseul a fost unul bine gândit: s-a schimbat scopul declarat al învățământului, apoi, în conformitate cu acest scop, s-au modificat planurile cadru, în conformitate cu acestea s-au alcătuit noi programe, după care s-au făcut noi manuale, alternative, după care s-au modificat metodele de predare și evaluare.
Manualele alternative analizate demonstrează cât se poate de clar că rezultatul acestei fuziuni – între redefinirea învățământului, programe, manuale și metode de predare și evaluare – este unul dezastruos pentru alfabetizarea matematică a elevilor. Noile practici și instrumente de lucru sunt structural și sistemic defectuoase, sunt inadecvate pedagogic și complet defazate intelectual, cu modul de a opera specific copiilor de anumite vârste. Debutul încâlcit și extrem de dificil – atât din pricina dificultății intrinseci a conținuturilor abordate, cât și din pricina metodei – nu face decât să sădească în copii ideea că matematicile sunt prea grele pentru ei, iar în părinți ideea că școala a devenit mai exigentă decât pe vremuri.
Această concluzie pe care o trag părinții elevilor de ciclu primar are două consecințe. În primul rând, îi împinge pe părinți și pe copii în brațele industriei meditațiilor, punând astfel o povară financiară foarte mare pe umerii părinților și o povară intelectuală prea mare pe umerii copiilor, obosindu-i sau făcându-i să-și piardă interesul pentru ceva ce nu pricep. În al doilea rând, le ascunde părinților modul în care, începând din gimnaziu și continuând cu liceul, elevii încep să bată pasul pe loc. Marea majoritate a părinților pot observa cât de grea e matematica de clasele primare, dar nu pot ține pasul cu fizica, matematica și chimia din gimnaziu, unde multe lucruri încep să se dilueze.
Impresia cu care rămân părinții din ciclul primar, cum că la școală e foarte greu, precum și obișnuința de a frecventa industria meditațiilor îi împiedică să vadă adevăratele cauze și metode care au făcut ca învățământul românesc pre-universitar să devină, ca și copiii lor, de nerecunoscut: pradă anarhiei intelectuale și incapabil să cultive valori.